Прямоугольный параллелепипед - это трехмерная геометрическая фигура, у которой все грани являются прямоугольниками. Для работы с этой фигурой важно понимать, как правильно вычислять основные параметры, включая сумму его измерений.
Содержание
Основные понятия
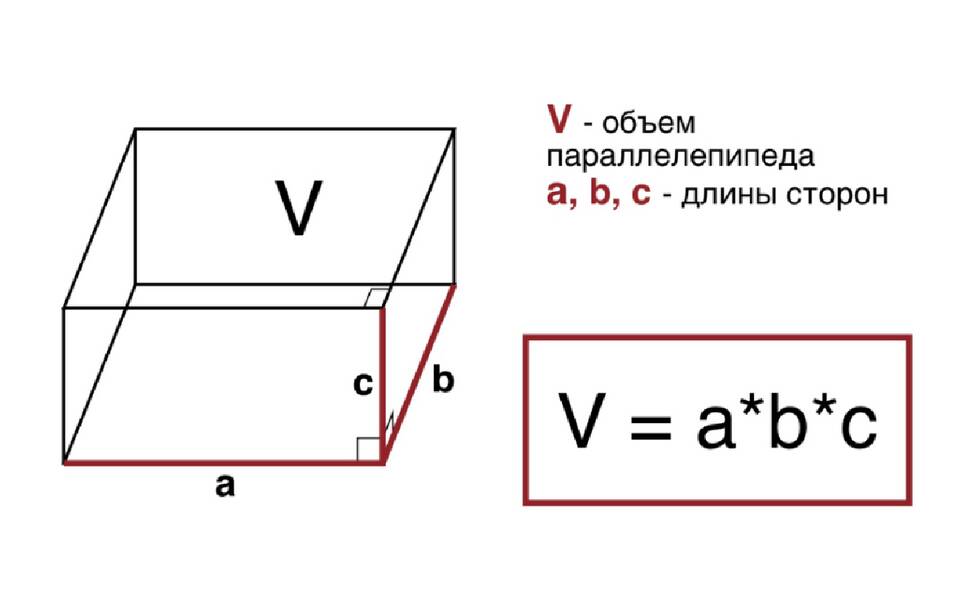
- Длина (a) - наибольшее измерение параллелепипеда
- Ширина (b) - среднее измерение
- Высота (c) - наименьшее измерение
- Сумма измерений - сумма всех линейных размеров
Формула суммы измерений
Основная формула
Сумма измерений = 4 × (a + b + c)
Пояснение формулы
| Компонент | Объяснение |
| 4 | Количество ребер каждого измерения |
| a | Длина параллелепипеда |
| b | Ширина параллелепипеда |
| c | Высота параллелепипеда |
Пошаговый алгоритм расчета
Измерение параметров
- Измерьте длину параллелепипеда (a)
- Измерьте ширину параллелепипеда (b)
- Измерьте высоту параллелепипеда (c)
- Убедитесь, что все измерения в одинаковых единицах
Вычисление суммы
- Сложите все три измерения: a + b + c
- Умножьте полученную сумму на 4
- Результат - общая сумма всех измерений параллелепипеда
Пример расчета
| Параметр | Значение (см) |
| Длина (a) | 10 |
| Ширина (b) | 5 |
| Высота (c) | 3 |
| Сумма измерений | 4 × (10 + 5 + 3) = 72 см |
Практическое применение
Где используется сумма измерений
- Расчет общего периметра всех ребер
- Определение количества материала для каркаса
- Оценка общей длины кромок при обработке
- Расчет длины соединительных элементов
Связь с другими параметрами
| Параметр | Формула |
| Площадь поверхности | 2 × (ab + ac + bc) |
| Объем | a × b × c |
| Пространственная диагональ | √(a² + b² + c²) |
Особые случаи
- Для куба (a = b = c): сумма измерений = 12a
- Для прямоугольной призмы с квадратным основанием: сумма измерений = 8a + 4c
- При наличии разных единиц измерения: необходимо привести к одной единице
Проверка правильности расчетов
- Сумма измерений всегда больше любого отдельного измерения
- Для куба результат должен делиться на 12
- При увеличении любого измерения сумма увеличивается